Adam's convergence proof is flawed
ICLR 2018 - 1st article
In this series, we explore the 2018 edition of the International Conference on Learning Representations. Oral papers are analyzed and commented in an accessible way.
This article is based on the paper On the convergence of Adam and beyond by Sashank J. Reddi, Satyen Kale, and Sanjiv Kumar.
If you asked people in the deep learning community what their favorite optimization algorithm is, you’d probably see Adam in the top 2 (with Stochastic gradient descent + momentum), far ahead of alternatives like Adagrad or RMSProp (we’ll come to these in a minute). Adam has become very popular in deep learning since it was proposed by Kingma & Ba in December 2014. The reasons are easy to understand: it exhibits impressive performance, uses many important ideas of previous works, comes with predefined settings that already work very well, and does not require careful hyper-parameter tuning. Better performance with less work, what more do you want?
Naturally, great power comes with great responsibilities, even for optimization algorithms like Adam. At the very least, we expect some theoretical guarantees on the convergence properties, to make sure that the algorithm is actually doing its job when required. This is a necessary sanity check, confirming by the maths that we can legitimately have faith in its correctness.
The convergence proof was provided in the original Adam paper. However, our authors show in their paper that this original proof is flawed, and Adam does not correctly converge in all problems, as illustrated by this theorem:
Theorem 3. [With mild assumptions on the parameters], there is a stochastic convex optimization problem for which Adam does not converge to the optimal solution.
How did we reach this point, where the most widely used optimization algorithm in deep learning does not converge in some simple convex problems? Let’s go back some years, and see what lead us there.
Gradient descent and adaptive methods
To facilitate analysis, let’s define our online optimization framework. At each time step $t$:
- The algorithm picks a point $x_t$ (weights of the model) in the feasible set $\mathcal{F}$.
- We then get access to the next mini-batch, with the associated loss function $f_t$, and we incur the loss $f_t(x_t)$.
Usually, our goal is to find an optimal parameter $x$ such that the loss $f(x)$ on the entire training set is minimal (intermediate loss functions $f_t$ are used as stochastic approximations of $f$). Here, in the (equivalent) online setup, the goal is to minimize the total regret at time $T$:
[R_T = \sum_{i=1}^T f_t(x_t) - \min_{x \in \mathcal{F}} \left(\sum_{i=1}^T f_t(x)\right)]
A large number of optimization algorithms were proposed to achieve this goal. For a detailed and intuitive overview (and introduction to gradient descent), I recommend this excellent blog post by Sebastian Ruder. We will just quickly go over a couple major steps that lead us to Adam.
- Mini-batch/Stochastic gradient descent is the first variant of gradient
descent that actually works decently well in deep learning. In our online setup,
it is reframed as online gradient descent, where the points $x_t$ are updated
by moving in the opposite direction of the gradient $g_t = \nabla f_t(x_t)$,
computed on the available mini-batch. The update size is determined by a
learning rate $\alpha_t$ (typically $\alpha/\sqrt{t}$ for some $\alpha$),
and the result is projected back to the feasible set thanks to the projection
operator $\Pi_{\mathcal{F}}$.
We thus get the update rule of SGD: $\ x_{t+1} = \Pi_\mathcal{F}(x_t - \alpha_t g_t)$.
Although the convergence of SGD requires a decreasing learning rate, choosing an adequate learning rate decrease schedule can be painful. Aggressive decays, such as $\alpha/\sqrt{t}$, or small learning rates, yield very slow convergence and mediocre performance. On the other hand, gentle decays and high learning rates yield very unstable training, even divergence sometimes. To overcome these issues, adaptive methods have been developed around the key idea that each weight, that is each coordinate of $x_t$, should be updated using its own learning rate, automatically computed based on the knowledge of past updates. This way, parameters that are frequently updated take only small steps (to avoid divergence), while parameters that are rarely updated take rather huge steps (to speed up convergence). This is summed up in the generic adaptive framework below:

We call $\alpha_t$ the step size, $\alpha_t/\sqrt{V_t}$ the learning rate, and restrict ourselves to diagonal variants $V_t = \text{diag}(v_t)$. This framework essentially allows us to compute a different learning rate for each weight, by rescaling the step size (common to all weights) with a function of past gradients (of the loss function with respect to the considered weight, thus weight-specific). Using this framework, we can follow the evolution of adaptive methods over time:
- (SGD) Stochastic gradient descent
$\phi_t(g_1, ..., g_t) = g_t\text{ }$ and $\text{ }\psi_t(g_1, ..., g_t) = \mathbb{I}$ SGD is also an adaptive method, with a specific strategy of not adapting at all: it forgets everything about the past of each weight, and relies only on the current gradient to perform the update, with a step size (and learning rate) $\alpha_t =\alpha/\sqrt{t}$, an aggressive decay.
- (AdaGrad) Adaptive gradient descent
$\phi_t(g_1, ..., g_t) = g_t\text{ }$ and $\text{ }\psi_t(g_1, ..., g_t) = {\text{diag}(\dfrac{1}{t} \sum_{i=1}^t g_i^2)}$ With the same step size $\alpha_t = \alpha/\sqrt{t}$, this yields an adaptive and much more reasonable learning rate of $\alpha/\sqrt{\sum_i g_{ij}}$ for a the $j$-th weight. When the gradients $\{g_{ij}\}$ are sparse, i.e. the $j$-th weight is not frequently updated, this considerably speeds up convergence (updates are still rare, but much bigger than with SGD).
- (RMSProp)
$\phi_t(g_1, ..., g_t) = g_t\text{ }$ and $\text{ }\psi_t(g_1, ..., g_t) = {\text{diag}((1-\beta)\sum_{i=1}^t \beta^{t-i} g_i^2)}$ Despite its huge benefits in some settings, AdaGrad tends to shrink the learning rates of frequently updated parameters, very quickly to virtually zero. To overcome this issue, RMSProp restricts the average of past gradients to a fixed window, instead of the entire past, to avoid shrinking the learning rates to virtually zero too quickly. In practice, this is implemented by an exponentially moving average of past gradients.
- (Adam) Adaptive momentum estimation
$\phi_t(g_1, ..., g_t) = (1-\beta_1)\sum_{i=1}^t \beta_1^{t-i} g_i^2{\ }\text{ }$ and $\text{ }\psi_t(g_1, ..., g_t) = {\text{diag}((1-\beta_2)\sum_{i=1}^t \beta_2^{t-i} g_i^2)}$ To further speed up the convergence, Adam adds to RMSProp the idea of momentum (instead of moving in the direction of the current gradient only, move in a direction that is a weighted average of current gradient and previous update, like a rolling ball’s movement is is influenced by the both the current slope and its momentum; see Ruder’s post). The momentum parameter $\beta_1>0$ considerably improves the performance of the algorithm, especially in deep learning. Combining momentum with adaptive methods, Adam is very efficient, and immensely popular.
The non-convergence of Adam
So, what’s wrong with Adam? It turns out that in the convergence proof given by Kingma & Ba, a flaw resides in the consideration of a specific quantity, namely:
[\ \Gamma_{t+1} = \left(\dfrac{\sqrt{V_{t+1}}}{\alpha_{t+1}} - \dfrac{\sqrt{V_{t}}}{\alpha_{t}}\right)]
Intuitively, $\Gamma_t$ measures the variations of the inverse of the learning rate. As we saw, convergence requires a non-increasing learning rate (otherwise the algorithm oscillates too much, or even diverges), which directly translates to $\Gamma_t \succeq O$ (easy to see with a diagonal $V_t$). This is the case for both SGD ($v_t$ constant, $\alpha_t$ decreasing) and AdaGrad ($v_t$ non-decreasing, $\alpha_t$ decreasing). However, it is no longer the case for Adam (nor RMSProp) because of the exponentially moving average of past gradients.
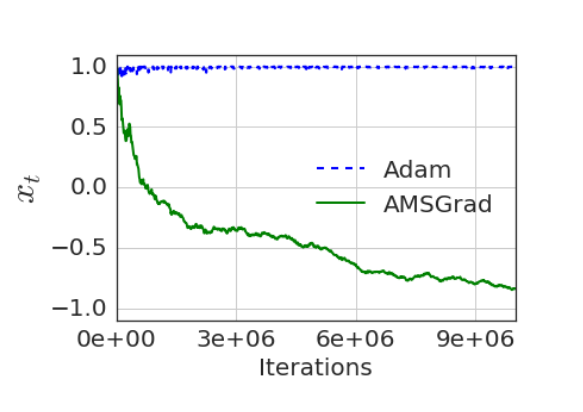
This is actually a huge issue, meaning that in some cases Adam actually converges to the worst solution possible. Following the example provided by the authors, consider $C>2$ and $\mathcal{F} = [-1,1]$, and the following losses:

The optimal solution would be $x=-1$. However, choosing $\beta_1 = 0$ and $\beta_2 = {1}/{(1+C^2)}$, Adam actually converges to the worst possible point $x = +1$. The intuition for this behavior is the following: although the algorithm observes a large gradient $C$ every $3$ steps, it forgets (scales down) this large gradient too quickly (due to the exponential weights) to counterbalance the wrong but most frequent updates.
So you thought Adam was reliable in all convex (“easy”) cases? Well, no:
Theorem 1. There is an online convex optimization problem where Adam has non-zero average regret.
Wait, but this is for a specific choice of parameters. We allowed the choice of a very small $\beta_2$, and to quote the paper, “this example also provides intuition for why large $\beta_2$ is advisable […], and indeed in practice using large $\beta_2$ helps”. So maybe we are safe when using correctly chosen parameters? Well, no:
Theorem 2. For any constant $\beta_1,\beta_2 \in [0,1)$ such that $\beta_1 < \sqrt{\beta_2}$ [typically satisfied by default settings], there is an online convex optimization problem where Adam has non-zero average regret.
All right, but this was in online optimization, where one could carefully design a sequence of loss functions to specifically fool Adam. We should be fine with stochastic optimization where such a design is impossible, right? Well, no:
Theorem 3. For any constant $\beta_1,\beta_2 \in [0,1)$ such that $\beta_1 < \sqrt{\beta_2}$ [typically satisfied by default settings], there is a stochastic convex optimization problem for which Adam does not converge to the optimal solution.
Now this is actually a major concern, since stochastic convex optimization is actually one of the simplest problems that we expect Adam to be able to solve (and deep learning consists mostly of non-convex stochastic optimization, which is reputed much harder). In practice, “fixing Adam” in cases of bad convergence behavior would typically require using different hyper-parameters for each dimension which, well, makes you wonder why you’re using adaptive methods in the first place (especially given the very high number of dimensions in typical deep learning applications).
Another important note is that this analysis remains valid for any adaptive method that is based on exponentially weighted moving averages (EWMA) of the gradients, including RMSProp, AdaDelta and NAdam, which are therefore also flawed.
AMSGrad, a new (and fixed) variant
Now that the maths have spoken and revealed the problem with Adam, what can be done? EWMA-based algorithms have actually brought a lot in terms of performance improvement and robustness to hyper-parameters choice, and it would be quite a pity to simply throw it all away for just a hole discovered in the proof.

To overcome this issue, the authors propose a new variant, AMSGrad, described in the algorithm above, that we explain in the next few lines. Remember that the issue with Adam resides in $\Gamma_t$, which should be semi-definite positive, while in some cases it is not because $\frac{v_{t+1, j}}{\alpha_{t+1}} - \frac{v_{t, j}}{\alpha_{t}} < 0$ for some index $j$. Well, a quick hotfix would be to replace $v_{t+1}$ by $\max(v_t, v_{t+1})$, which would ensure $\Gamma_t \succeq 0$. But this would bias our computations of the EWMA… However we can decouple the two processes by keeping two running variables: one “true” running variable $v_{t+1}$ used to accurately compute the EWMA (correctly accounting for the past), and one “used-in-updates” running variable ${\hat v_{t+1}} = {\max(v_{t+1}, \hat v_t)}$ used to ensure a non-increasing learning rate (hence the correctness of the algorithm).
Theoretical justifications of AMSGrad back up this claim: for reasonable choices of parameters, the regret is bounded in $O(\sqrt{T})$. Additionally, for a specific choice of momentum decay $\beta_{1t} = \beta_1 \lambda^{t-1}$, the authors prove a bound on the regret that can hugely benefit from sparse gradients, potentially “considerably better than $O(\sqrt{dT})$ regret of SGD”.
Does this translate into good empirical performance? The paper provides the convergence curves for a synthetic example that is close to the previous example (with $\mathcal{F} = [-1, 1]$, the optimal solution being $x=-1$):


This example shows that AMSGrad works on the synthetic example where Adam fails to converge to the true solution, which is always a good sign, since it was why it was designed in the first place. But what about standard convergence benchmarks on more interesting problems, like logistic regression or neural networks? Reddi et al. provide graphics that claim for AMSGrad equal or better performance compared to Adam for logistic regression, feed-forward neural net (1 hidden layer) on MNIST, and CIFARNET. However, in an independent implementation by Filip Korzeniowski tested in various settings (you should definitely check his post for extensive details and comparisons), the experiments do not support any claim of practical difference between Adam and AMSGrad. We show below the validation accuracy (what we care about in the end) he gets for both algorithm on CIFAR-10.
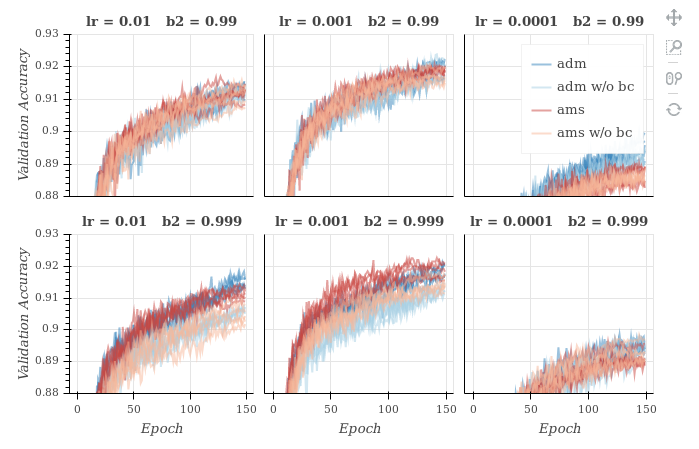
Validation accuracy on CIFAR-10
(VGG-16).
Adam in blue, AMSGrad in red.
Does it matter?
In my opinion, it is pretty clear that the main interest of the paper lies in pointing out the flaw in Adam’s proof, and how it affects the convergence behavior in some cases. AMSGrad sounded somewhat more like a hotfix than a real replacement, providing a sounder algorithm while maintaining Adam’s good performance. AMSGrad will not change the course of stochastic optimization’s (nor deep learning’s) history, may it even come to someday replace Adam in practice. In the end, it doesn’t even matter (that much) ; a true “breakthrough” replacement is yet to come.
What is more interesting is the meta-aspect of the proof-checking side of this paper. It seems very important to me that empirical observations of bad convergence behavior are finally backed up by theoretical justifications, in other words, that someone finally checked the maths. I find it actually surprising that despite its “reasonable” length of 4 pages, no one checked the proof and spotted this mistake, while in the meantime Adam got increasingly popular and widely used. Note that I barely ever read the proofs myself. I would tend to link this phenomenon to a deeper trend in the machine/deep learning community: people (and scientists are people too) get really excited about the results, the performance and the new opportunities brought by an exponentially growing field, and we just forget how to do good science along the way. The reproducibility crisis denounced by researchers like Joëlle Pineau (especially in reinforcement learning) is one example; the fact that everyone skips the proofs to go straight to the next exciting paper is another.